Rashi on 6;16 explains that "And to a cubit finish it from above" refers to a sloped roof which narrowed at the top and was 1 cubit high at the topmost point, allowing the water to flow downward off the roof on both sides.
The idea for this post developed when I was working with a student on a different math project related to the ark. This was a question that arose, but since she was focused on a different mathematical concept, she chose not to pursue the question below. Since our conversation last year, I've been looking forward to investigating this question for this parsha.
Pythagorean Theorem:
The Pythagorean Theorem is a theorem that we use when calculating with right triangles (triangles that have a right or 90° angle).
In the diagram above, we have a right triangle with legs a and b and hypotenuse c. In a right triangle, the hypotenuse is always the longest side and it is always the side across from the right angle. The legs are the two sides that join together to make the right angle. In our diagram, around the sides of the triangle are squares. Each square is made from sides that are the lengths of the three sides of the triangle. The Pythagorean Theorem tells us that if you take the squares of a and b, the areas of those two squares can be used to make up the exact same area as the square of c. Mathematically, for older students, this concept is easily written out as:
a2 + b2 = c2
For younger students, if they are able to calculate a number multiplied by itself, then they can make the calculations to figure out the areas of these squares.
For practical calculation purposes, if you know any two sides of a right triangle, you can use this theorem to calculate the missing third side.
Parsha Connection:
We are given specific dimensions for the construction of the ark:
*length- three hundred cubits
*width- fifty cubits
*height- thirty cubits
However, we are also told that the roof should be 1 cubit high and, according to Rashi, it slopes for the flow of water off the roof. Essentially, the roof is created in the form of an isosceles triangle (a triangle with at least 2 sides of equal length), with the vertex of the triangle up at the top of the ark.
Using what we know about the dimensions of the ark and the Pythagorean Theorem, how can we figure out the width of the wood needed to form the two sloping sides of the roof?
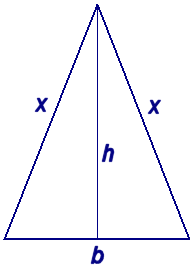
Let's visualize a view of the roof from the front of the ark.
If we're looking head-on, this could be a sketch of the roof of the ark:
*The 2 sides, x, would be each of the two sloping sides of the roof.
*The height, h, at the center, would be the 1 cubit height that is described in the parsha.
*The bottom, b, would be the width from one side of the ark to the other- 50 cubits, as described in the parsha.
But how does this help us? This is an isosceles triangle. We know that the Pythagorean Theorem only applies to right triangles. If you look carefully at the triangle above, you can see that we can actually break the isosceles triangle into two congruent (exactly the same) triangles- if we cut the isosceles triangle along the height line, h, then we have two congruent right triangles. The legs of the triangle will be h and half of the bottom b; the hypotenuse of each triangle will be the slopes- x.
Let's put this information back into the format for the Pythagorean Theorem:
The a will be replaced with our h- the height line.
*Remember we said that h was the height given in the parsha- 1 cubit.
The b will be replaced with our new b number- 1/2 of the width distance b.
*Remember we said that this was the width given in the parsha- the full width of the ark was 50 cubits, so half of that width (to calculate for the right triangle) is 25 cubits.
The c will be replaced with our x- the slopes of the roof.
*This is the missing information that we're looking for.
So, now we can put our own numbers into the set-up for calculation:
a2 + b2 = c2
h2 + b2 = x2
12 + 252 = x2
Now we calculate:
12 = 1
252 = 625
So, 1 + 625 = x2
626 = x2
Now we need to know what number multiplied by itself will give us 626. For older students, they would either use a square root function, or, by hand, they could use prime factorization to possibly calculate the number. Younger students might use guess, check, and correct to narrow down the number to an approximate length.
If we just look at the numbers, we know that 252 = 625, and we're looking at 626- a number very close. Just by looking at it, we can see that the length of the sloped side will be very close to 25 cubits, but a little bit longer (since 626 is larger than 625).
If we actually calculate the square root using a calculator, we get 25.02 cubits (if we round the number).
If we calculate using prime factorization, we get that 626 = 2 x 313. Since these are both prime numbers, this doesn't help us to come to a number.
So, with our calculation, we know that the pieces for the sloped roof of the ark needed to be approximately 25.02 cubits wide. The complete measurements of these sloped pieces needed to be 300 cubits long (to reach from front to back of the ark) and 25.02 cubits wide to reach from the tip of the roof down to the top of the sides of the ark.
Everyday Connection:
The world is a spacial environment. We have squares and rectangles all around us. Do you know that if you break squares and rectangles in half by making a diagonal cut from one upper corner to the opposite bottom corner you are actually creating two congruent right triangles? That length of the horizontal cut is actually the hypotenuse of each of those right triangles. Did you know that TV and computer monitor sizes are actually measured by that hypotenuse length?
An activity for younger students is a geometry scavenger hunts, where they need to list different shapes that they see in the world around them and connect them to what they've learned in class. This can actually be done at any age and really helps students open their eyes to how the material they are learning is part of their environment. What triangles do you see around you every day?

No comments:
Post a Comment