Lech Lecha- Vectors and Velocity

"Hashem appeared to Avram and said, 'To your offspring I will give this land.' So he built an altar [in Canaan] to Hashem Who appeared to him. From there he relocated to the mountain east of Beth-el and pitched his tent, with Beth-el on the west and Ai on the east; and he built there an altar to Hashem and invoked Hashem by Name. Then Avram journeyed on, going and traveling toward the south. There was a famine in the land, and Avram descended to Egypt to sojourn there, for the famine was severe in the land." ~Bereishit 12;7-10
"So Avram went up from Egypt, he with his wife and all that was his- and Lot with him- to the south. Now Avram was very heavy with livestock, with silver, and with gold. He proceeded on his journeys from the south to Beth-el, to the place where his tent had been at first, between Beth-el and Ai, to the site of the altar which he had made there at first; and there Avram invoked Hashem by Name." ~Bereishit 13;1-2

Vectors:
In their introductory to Geometry, younger students are introduced to the concepts of points, lines, line segments, and rays.
*A point is a single point or location.
*A line is a straight connection between two points that continues straight and extends indefinitely in both directions
*A line segment is the straight connection between two points with endpoints at the two points
*A ray is the straight connection between two points with an endpoint at one of the points and extending indefinitely through the other point

 A vector is a concept that is not classically introduced to younger students. Essentially, a vector is the same idea as a segment, but it also includes information about distance and tells which direction you're moving in. The two key aspects to a vector are distance (referred to as "magnitude") and direction. Velocity explains the speed at which something is moving (again, it's magnitude) and the direction in which it is moving (23 miles per hour NorthEast). With this understanding of vector and velocity, we can see that velocity is a type of vector measurement, and we can use this understanding to measure how far something travels and the direction in which it is traveling. One simple example would be calculating how far something is traveling either towards (+) or away from (-) a given point. To think about vectors in their simplest form, every straight movement in one direction can be shown as one vector. This means that if I'm traveling in one direction, and then I change my direction, I would need to use 2 different vectors- 1 to explain the first part of my trip, and 1 to explain my trip after I change my direction.

The vector label is based on directions relative to a specific reference point. It's important to realize that this information only tells you have far and in what direction you've moved from your starting point; by itself it doesn't tell you how close or far you are from your reference point. In order to know where you are related to your reference point, you need to add or subtract different vectors to calculate the distance. Using the calculations of multiple vectors, this type of information can be charted on graphs showing distance compared to a location over time on a coordinate plane, and adding the aspect of direction adds an additional quality of information to the graph. For today, we'll just look at simple vectors.

Parsha Connection:
In this week's parsha, we learn of Avram's travels over the course of 25 years. If we look specifically at his travel from the beginning of the 12th chapter through the beginning of the 13th chapter of Bereishit, we see him set-up his tent in Canaan between Beth-el and Ai, travel down to Egypt for the duration of a famine, and then travel back up to return to the exact same location between Beth-el and Ai. How can we use vectors or velocity to explain his trip?

Based on a rough estimate found here, let's assume that Avram's travel distance for his trip from Beth-el down to Egypt was approximately 225 miles. If we designate Beth-el as his starting point (the location where he wants to be) and we use the standard of North and East representing positive directions and South and West representing negative, then his trip down to Egypt is mileage expressed as a negative velocity. So, for example, he starts at 0 miles (when he's standing in Beth-el), and after traveling 100 miles towards Egypt, he had traveled 100 miles SouthWest, or -100 miles, because he was moving away from Beth-el in a negative direction. When he reached his final destination in Egypt, he had traveled 225 miles SouthWest, or -225 miles. On his return trip, he is now heading NorthEast, which is a positive direction. As he traveled back toward Beth-el, let's say he traveled 60 miles per day (velocity = 60 mph NE)- assuming he was traveling by camel.
*After 1 day, he was 60 miles closer to Beth-el, so he had traveled 60 miles NorthEast, or +60 miles
*After 2 days, he was another 60 miles closer, so he had traveled 120 miles NorthEast, or +120 miles
*After 3 days, he was another 60 miles closer, so he had traveled 180 miles NorthEast, or +180 miles
*On his 4th day, he covered the final 45 mi to reach his destination, and he stopped once he reached his 225 miles NorthEast, or +225 miles, to get to Beth-el.

Note that you can see here that by adding the individual vectors from each day, we get an accumulated larger vector, only because Avram was continuing his travel in the exact same direction. 

Extension Thoughts:
If we add the two vectors from each trip together, we get zero - he's back to his initial starting point. (-225 miles) + (+225 miles) = 0 miles. If we add the vectors after the first day of Avram's return trip, his total travels still end up as a negative vector. He travelled 225 miles SouthWest, and then 60 miles NorthEast. (-225 miles) + (+60 miles) = (-165 miles), or 165 miles SouthWest of the vector's starting point.

Everyday Activity:
The concept of vectors can be quite easily integrated into younger students learning about measurement and distance. Simple classroom activities can include students measuring distance from a reference point and then having them walk certain distances in directions related to your reference point and expressing their walks using vector language.

A simple everyday example of vectors: Have you ever paid attention to the highway distance markers as you drive along? Using those markers, you can say that you've driven 23 miles North toward your destination.

Noah- Geometry & Pythagorean Theorem

"G-d said to Noah, 'The end of all flesh has come before Me, for the earth is filled with robbery through them; and behold, I am about to destroy them from the earth. Make yourself an ark of gopher wood; make the ark with compartments, and tar it inside and out with pitch. This is how you should make it- three hundred cubits the length of the ark; fifty cubits its width; and thirty cubits its height. A light shall you make for the ark, and to a cubit finish it from above. The entrance of the ark you shall put in its side; make it with bottom, second, and third decks...'" ~Bereishit 6;13-16

Rashi on 6;16 explains that "And to a cubit finish it from above" refers to a sloped roof which narrowed at the top and was 1 cubit high at the topmost point, allowing the water to flow downward off the roof on both sides.

The idea for this post developed when I was working with a student on a different math project related to the ark. This was a question that arose, but since she was focused on a different mathematical concept, she chose not to pursue the question below. Since our conversation last year, I've been looking forward to investigating this question for this parsha.

Pythagorean Theorem:
The Pythagorean Theorem is a theorem that we use when calculating with right triangles (triangles that have a right or 90° angle).

In the diagram above, we have a right triangle with legs a and b and hypotenuse c. In a right triangle, the hypotenuse is always the longest side and it is always the side across from the right angle. The legs are the two sides that join together to make the right angle. In our diagram, around the sides of the triangle are squares. Each square is made from sides that are the lengths of the three sides of the triangle. The Pythagorean Theorem tells us that if you take the squares of a and b, the areas of those two squares can be used to make up the exact same area as the square of c. Mathematically, for older students, this concept is easily written out as:

a² + b² = c²

For younger students, if they are able to calculate a number multiplied by itself, then they can make the calculations to figure out the areas of these squares.

For practical calculation purposes, if you know any two sides of a right triangle, you can use this theorem to calculate the missing third side.

Parsha Connection:

We are given specific dimensions for the construction of the ark: 

*length- three hundred cubits 

*width- fifty cubits

*height- thirty cubits

However, we are also told that the roof should be 1 cubit high and, according to Rashi, it slopes for the flow of water off the roof. Essentially, the roof is created in the form of an isosceles triangle (a triangle with at least 2 sides of equal length), with the vertex of the triangle up at the top of the ark. 

Using what we know about the dimensions of the ark and the Pythagorean Theorem, how can we figure out the width of the wood needed to form the two sloping sides of the roof?

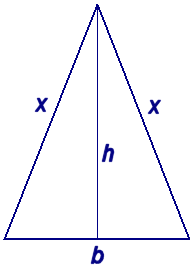
Let's visualize a view of the roof from the front of the ark.

If we're looking head-on, this could be a sketch of the roof of the ark:

*The 2 sides, x, would be each of the two sloping sides of the roof. 

*The height, h, at the center, would be the 1 cubit height that is described in the parsha.

*The bottom, b, would be the width from one side of the ark to the other- 50 cubits, as described in the parsha.

But how does this help us? This is an isosceles triangle. We know that the Pythagorean Theorem only applies to right triangles. If you look carefully at the triangle above, you can see that we can actually break the isosceles triangle into two congruent (exactly the same) triangles- if we cut the isosceles triangle along the height line, h, then we have two congruent right triangles. The legs of the triangle will be h and half of the bottom b; the hypotenuse of each triangle will be the slopes- x. 

Let's put this information back into the format for the Pythagorean Theorem:

a² + b² = c<sup>2

The a will be replaced with our h- the height line.
*Remember we said that h was the height given in the parsha- 1 cubit.
The b will be replaced with our new b number- 1/2 of the width distance b.
*Remember we said that this was the width given in the parsha- the full width of the ark was 50 cubits, so half of that width (to calculate for the right triangle) is 25 cubits.
The c will be replaced with our x- the slopes of the roof.
*This is the missing information that we're looking for.</sup>

So, now we can put our own numbers into the set-up for calculation:
a² + b² = c²
h² + b² = x²
1² + 25² = x<sup>2

Now we calculate:</sup>
1² = 1
25² = 625

So, 1 + 625 = x²
626 = x<sup>2

Now we need to know what number multiplied by itself will give us 626. For older students, they would either use a square root function, or, by hand, they could use prime factorization to possibly calculate the number. Younger students might use guess, check, and correct to narrow down the number to an approximate length.</sup> 

If we just look at the numbers, we know that 25² = 625, and we're looking at 626- a number very close. Just by looking at it, we can see that the length of the sloped side will be very close to 25 cubits, but a little bit longer (since 626 is larger than 625).

If we actually calculate the square root using a calculator, we get 25.02 cubits (if we round the number).
If we calculate using prime factorization, we get that 626 = 2 x 313. Since these are both prime numbers, this doesn't help us to come to a number.

So, with our calculation, we know that the pieces for the sloped roof of the ark needed to be approximately 25.02 cubits wide. The complete measurements of these sloped pieces needed to be 300 cubits long (to reach from front to back of the ark) and 25.02 cubits wide to reach from the tip of the roof down to the top of the sides of the ark.

Everyday Connection:
The world is a spacial environment. We have squares and rectangles all around us. Do you know that if you break squares and rectangles in half by making a diagonal cut from one upper corner to the opposite bottom corner you are actually creating two congruent right triangles? That length of the horizontal cut is actually the hypotenuse of each of those right triangles. Did you know that TV and computer monitor sizes are actually measured by that hypotenuse length? 

An activity for younger students is a geometry scavenger hunts, where they need to list different shapes that they see in the world around them and connect them to what they've learned in class. This can actually be done at any age and really helps students open their eyes to how the material they are learning is part of their environment. What triangles do you see around you every day?

Bereishit- Place Value and Regrouping

Addition and Place Values:
When younger children begin learning to add (and subtract) multi-digit numbers, the algorithms alone for these calculations can be confusing. As a starting point, children first need to understand the meaning behind what each digit in a number represents. As they expand their understanding, it is helpful for children to recognize the pattern of every three place values from the decimal point moving towards the left. Larger decimal place values come later, but, again, understanding the pattern of place value will help students pick up the larger picture of what's happening with the numbers.

Basic place values to the millions:

The biggest hurdle for students to overcome is that each place value can't have more than 9 of it's kind, and every time you reach a group of 10, you have reached the next place value and need to "regroup" your numbers.

*10 ones = 1 ten and 0 ones [10]
*10 tens = 1 hundred and 0 tens and 0 ones [100]
*10 hundreds = 1 thousand and 0 hundreds and 0 tens and 0 ones [1,000]
*10 thousands = 1 ten-thousand and 0 thousands and 0 hundreds and 0 tens and 0 ones [10,000]
*10 ten-thousands = 1 hundred-thousand and 0 ten-thousands and 0 thousands and 0 hundreds and 0 tens and 0 ones [100,000]
*10 hundred-thousands = 1 million and 0 hundred-thousands and 0 ten-thousands and 0 thousands and 0 hundreds and 0 tens and 0 ones [1,000,000]

It helps for children to visualize this concept using manipulatives such as base-10 blocks, which have models for ones, tens, hundreds, and thousands. Paper clips are a good make-shift manipulative, since students can clip and unclip into and out of groups of 10, 100, etc. as they make sense of the numbers.

One key that is critical for students to remember is that they need to line up the place values- you can only add ones with ones, tens with tens, hundreds with hundreds, etc. (and then regroup as needed).

Parsha Connection:
Chapter 5 of this week's parsha gives details of the direct lineage from Adam to Noah. We are given information on names and ages for this direct line of descendants. We are given enough information about each person to provide 9 sample addition problems, where we can check the numbers that we are given in the parsha.

As a first step, let's organize the individual pieces of information that we are given. As we organize information for each person, we can check the math.

1st generation:
"This is the account of the descendants of Adam- on the day of G-d's creating of Man, He made him in the likeness of G-d. He created them male and female. He blessed them and called their name Man on the day they were created- when Adam had lived one hundred and thirty years, he begot in his likeness and his image, and he named him Seth. And the days of Adam after begetting Seth were eight hundred years, and he begot sons and daughters. All the days that Adam lived were nine hundred and thirty years; and he died." ~Bereishit 5;1-5

Adam was 130 years old when Seth was born.
Adam lived 800 years after Seth was born.
Adam died at 930 years old

  130
+800 
  930    so this works

2nd generation:
"Seth lived one hundred and five years and begot Enosh. And Seth lived eight hundred and seven years after begetting Enosh, and he begot sons and daughters. All the days of Seth were nine hundred and twelve years; and he died." ~Bereishit 5;6-8

Seth was 105 years old when Enosh was born.
Seth lived 807 years after Enosh was born.
Seth died at 912 years old

  105
+807
  912    so this works

The above example offers regrouping in the ones (to tens) digits.

3rd generation:
"Enosh lived ninety years, and begot Kenan. And Enosh lived eight hundred and fifteen years after begetting Kenan, and he begot sons and daughters. All the days of Enosh were nine hundred and five years; and he died." ~Bereishit 5;9-11

Enosh was 90 years old when Kenan was born.
Enosh lived 815 years after Kenan was born.
Enosh died at 905 years old

   90
+815
  905    so this works

The above example offers a sample with different sized numbers (one tens and one hundreds), which offers a good check on understanding lining up the place values. Also, we have regrouping in the tens (to hundreds) digits here.

4th generation:
"Kenan lived seventy years, and begot Mahalalel. And Kenan lived eight hundred and forty years after begetting Mahalalel, and he begot sons and daughters. All the days of Kenan were nine hundred and ten years; and he died." ~Bereishit 5;11-14

Kenan was 70 years old when Mahalalel was born.
Kenan lived 840 years after Mahalalel was born.
Kenan died at 910 years old

   70
+840
  910    so this works

Again, here we have different sized numbers and regrouping in the tens (to hundreds) digits.

5th generation:
"Mahalalel lived sixty-five years, and begot Jared. And Mahalalel lived eight hundred and thirty years after begetting Jared, and he begot sons and daughters. All the days of Mahalalal were eight hundred and ninety-five years; and he died."  ~Bereishit 5;15-17

Mahalalel was 65 years old when Jared was born.
Mahalalel lived 830 years after Jared was born.
Mahalalel died at 895 years old

   65
+830
  895    so this works

Again, here we have different sized numbers.

6th generation:

"Jared lived one hundred and sixty-two years, and begot Enoch. And Jared lived eight hundred years after begetting Enoch and he begot sons and daughters. All the days of Jared came to nine hundred and sixty-two years; and he died." ~Bereishit 5;18-20

Jared was 162 years old when Enoch was born.
Jared lived 800 years after Enoch was born.
Jared died at 962 years old

  162
+800
  962    so this works

7th generation:
"Enoch lived sixty-five years, and begot Methuselah. Enoch walked with G-d for three hundred years after begetting Mehuselah; and he begot sons and daughters. All the days of Enoch were three hundred and sixty-five years. And Enoch walked with G-d; then he was no more, for G-d had taken him." ~Bereishit 5;21-24

Enoch was 65 years old when Methuselah was born.
Enoch lived 300 years after Methuselah was born.
Enoch died at 365 years old

   65
+300
  365    so this works

8th generation:

"Methuselah lived one hundred and eighty-seven years and begot Lamech. And Methuselah lived seven hundred and eighty-two years after begetting Lamech, and he begot sons and daughters. All the days of Methuselah were nine hundred and sixty-nine years; and he died." ~Bereishit 5;25-27

Methuselah was 187 years old when Lamech was born.
Methuselah lived 782 years after Lamech was born.
Methuselah died at 969 years old

  187
+782
  969    so this works

Again, here we have regrouping in the tens (to hundreds) digits.

9th generation:
"Lamech lived one hundred and eighty-two years, and he begot a son. And he called his name Noah, saying, 'This one will bring us ease from our work and from the toil of our hands, from the ground which Hashem had cursed.' Lamech lived five hundred and ninety-five years after begetting Noah, and he begot sons and daughters. All the days of Lamech were seven hundred and seventy-seven years; and he died." ~Bereishit 5;28-31

Lamech was 182 years old when Noah was born.
Lamech lived 595 years after Noah was born.
Lamech died at 777 years old

  182
+595
  777    so this works

Again, here we have regrouping in the tens (to hundreds) digits.

10th generation:
"When Noah was five hundred years old, Noah begot Shem, Ham, and Japheth." ~Bereishit 5;32

Noah was 500 years old when Shem, Ham, and Japheth were born.

Follow-up Activities:
If you take this base information and use it to try to place the births and deaths in a timeline, students can calculate how old each person was at the births of successive descendants, as well as how old each of the descendants was at the time of death of their ancestors. These calculations will offer students more, similar calculation practice.

For an added exercise, having students identify which numbers to use for these different comparative calculations offers practice with problem solving and identifying important information.

V'Zot HaBracha- Math Related Grammar

This Shabbat, being Chol HaMoed Sukkot, we will be reading a portion from parshat Ki Tisa. However, since next week we read V'Zot HaBracha and Bereishit in the same week, I felt it would be appropriate to appropriate V'Zot HaBracha for this week, and continue with Beresheit next week.

"And He became King over Yeshurun when the numbers of the nation are gathered- the tribes of Israel in unity." ~Devarim 33;5 

Rashi on 33;5 explains that it says "numbers of the nation" referring to when the nation gathers and is unified, they are worthy of being individually counted and being blessed by Hashem.

Mathematical Grammar:
If you are a person who is aware of proper grammar, you may have noticed that there are certain words that many people misuse on a regular basis. If the grocery store sign "12 items or less" has ever bothered you, then you have an awareness of mathematical grammar. To be accurate, the sign should read "12 items or fewer". What's the difference? There are certain words that relate specifically to countable quantities, while their counterpart words, which are often mistakenly used, actually relate to non-countable quantities (although there are exceptions where one word can be used for both).

What does this mean?

Consider asking, "Do you want more or less soup?" as opposed to "Do you want more or fewer pretzels?" Less applies to soup- a non-countable item, while fewer applies to pretzels- a countable item. If you were to switch and use fewer with the soup question or less with pretzels, it doesn't sound nearly as smooth, because the wording isn't right.

Another such word pair example is many and much. Would you ask "How many soup would you like?" or would you ask "How much soup would you like?". Consider the pretzels- "How many pretzels?" or "How much pretzels?". Again, many applies to the countable item, while much  refers to the non-countable quantity.

Parsha Connection:
If the Torah were talking about the nation- it would be referred to as a single unit- "when the nation is gathered". Rather, we are told of when the "numbers of the nation are gathered"- clearly referring to countable individuals- because when the nation is in perfect unity, each individual within the nation is worthy of being counted and blessed.

Think about referring to a change in size of the nation. We would speak of more or fewer people, but when referring to the nation as a whole, we would speak of the nation being larger or smaller. Again, more/fewer people refer to a countable entity, while larger/smaller nation is a non-countable quantity.

Yom Kippur- Shofar Blasts and Equivalent Fractions

The parsha that we read on Yom Kippur comes from a section of Acharei Mot. My previous post from Acharei Mot covers the topic of the two goats that were brought for atonement by the Kohen Gadol on behalf of the Jewish people on Yom Kippur.

As one feature characteristic of this time of year is the blowing of the shofar, I thought I would look at the shofar blowing this week. The month of Elul leading up to Rosh Hashana, then the first 10 days of Tishrei- the days of atonement between Rosh Hashana and Yom Kippur- we listen to the shofar. Throughout Elul, we hear the shofar blown once each day. On Rosh Hashana, we hear 100 blasts of the shofar on both days. On Yom Kippur, we hear a final shofar blast at the end of the day.

Equivalent Fractions:

Equivalent fractions are different ways of writing the same fractional piece of a whole item (or group). They are two or more fractions that represent the same amount of an item but are written with different numerators and denominators. We can find these fractions by breaking the whole item into more or fewer pieces. The important thing to look for is that when you cut it into more pieces, a certain number of those pieces has to exactly create a larger piece. 

For example, [Case 1] if I have a pizza and I cut it into two pieces and eat one of the pieces, then I've eaten 1/2 of the pizza. Now, [Case 2] if I had cut the pizza into 4 pieces and eaten 2 of the pieces, then I would have eaten 2/4 pieces, which is actually the same amount of pizza as in Case 1. [Case 3] If I had cut the pizza into 6 pieces and eaten 3 of the pieces, then I would have eaten 3/6, which is, again, actually the same amount of pizza as in the first two cases. But now, what if I had cut the pizza into 3 pieces, or 5 pieces? In these two situations, we could not take a number of pieces to make them exactly 1/2 of the pizza. So, we can make equivalent fractions with 1/2 using fourths and sixths, but we can't find equivalent fractions using thirds or fifths.

Shofar Connection:

From the time that young children begin learning about the shofar blasts, they are taught that there are 3 different types of blasts: tekiah, shevarim, and teruah. They learn that tekiah is one long blast, shevarim is 3 shorter blasts, and teruah is 9 staccato blasts. 

(artwork credit to my preschool daughter)

If we think about these blasts as fractions, we can consider that tekiah is one whole blast (one single unit), the 3 parts of the shevarim blast are each 1/3 of the length of the tekiah, and the 9 parts of the teruah blast are each 1/9 the length of the tekiah. If we look further, we can also compare that each group of 3 blasts of teruah is the same as 1 of the shevarim sections. In other words, we can see that 1/3 of the shevarim blast is equivalent to 3/9 of the teruah blast.

In theory, this is all nice, but how do we quantify the blasts? What measurements do we use? Are they actually equivalent fractions? I checked with my husband on this- our local shofar blower (ba'al tokeah)- to get an answer. Below is a purely theoretical example of how it should work with the blasts measured in seconds.

Note: I'm purposely using numbers here that are slightly larger than in practice to make calculations easier)

If Tekiah is set to 9 seconds, then Shevarim is also set to 9 seconds for the whole blast (so the total is equivalent to tekiah), which means that each 1/3 section must be 3 seconds to be considered kosher.

Teruah would also be set to 9 seconds for the whole blast (so the total is equivalent to tekiah and shevarim), which means that each 1/9 section must be 1 second (and 3 sections together equal 3 seconds to be equivalent to a 1/3 shevarim section) to be considered kosher.

These would work for both "tekiah-shevarim-tekiah" and "tekiah-teruah-tekiah" blasts. Since the middle section cannot be longer than the tekiah itself, we would need to adjust for the "tekiah-shevarim/teruah-tekiah". For these blasts, the tekiah would be set to 12 seconds, and the shevarim/teruah together would need to be 12 seconds, so shevarim would be 6 seconds (2 seconds for each short blast), and teruah would be 6 seconds (6/9 or 2/3 of a second for each of the staccato blasts).

Now, in practice, when my husband blows shofar, our Rabbi watches with a stop watch to make sure that the shofar blasts are, in fact, fractional pieces of each other. What does this look like in practice?

The first thing to keep in mind is that practical situations are variable, and it's better to overestimate the length of a blast in order to make sure that it's kosher. Basically, when you have a kosher blast, you want to be able to count it. In order to do this, the procedure is basically as follows:

Since we can't predict the exact time in seconds that the middle blasts will be (shevarim, teruah, and shevarim/teruah), we overestimate on the time length for the first tekiah to make sure that the total length of that middle blast is always about the same length as the tekiah, but never longer than the tekiah. Since, for the final tekiah, you know exactly how long the middle blasts took, the final tekiah is timed to be exactly as long as the middle section. Also, since holding 100 shofar blasts for 10-12 seconds is extremely wearing, the blasts are actually shorter (and do not use quick, simple numbers), which makes a lot of the calculations involve fractions of seconds. 

So, in real life, the blasts look something like this:

For "tekiah-shevarim-tekiah", the first tekiah is overestimated at about 5 seconds, the goal for shevarim is to have 3 1-1/2 second sections, making the whole shevarim 4-1/2 seconds long, and the final tekiah is 4-1/2 seconds.

For "tekiah-teruah-tekiah", the first tekiah is overestimated at about 6 seconds, the goal for the teruah is to have 9 sections that are just over 1/2 second each (5/9 of a second), making the whole teruah 5 seconds long, and the final tekiah is 5 seconds.

For "tekiah-shevarim/teruah-tekiah", the first tekiah is overestimated at about 9 seconds, the goal for the shevarim/teruah is to have 3 1-1/3 second blasts for the shevarim (4 seconds total for that part) and 9 sections that are just under 1/2 second each (4/9 of a second) for the teruah (4 seconds total), making the total shevarim/teruah 8 seconds long, and the final tekiah is 8 seconds long.

What does this mean about the tekiah gedolah (the long tekiah at the end of the 100 blasts)? My husband tries to make that one 12 seconds. Why 12 seconds? Because this would be equivalent to 1 estimated tekiah length from the shevarim/teruah set, plus another 1/3 or another 3 seconds, since that additional fractional amount is enough to make it noticeably longer than the other blasts.

Best wishes for a G'mar Chatima Tova- a sealed inscription for a year filled with only good things.